How to improve on a guess
Guessing (aka intuition or expert judgement) is probably the most common method of estimating that we use, but also the most inaccurate.
Most people fall into the trap of giving a single answer when asked for an estimate. Don’t. Instead, offer a minimum (lower bound) and maximum (upper bound) AND a confidence rating of 90%. Your range should be neither too wide nor too narrow: it should be wide enough so that, in your best judgement, the range gives a 90% chance of including the right answer.
For example, if I asked you to give me an estimate for the average rainfall in September, you might initially say “I have no idea”. But that is not true; you have some idea of what the answer might be. As Douglas Hubbard says, “There is literally nothing we will likely ever need to measure where our only bounds are negative infinity to positive infinity.” I may say something like “I am 90% confident that the rainfall in September will be between 0mm and 100mm”.
“The lack of having an exact number is not the same as knowing nothing” ~ Douglas Hubbard
How good are we at guessing?
Unfortunately, it appears that we are not naturally very good at guess-timates even when using ranges. Both Douglas Hubbard and Steve McConnell have run multiple experiments that show most of us are over-optimistic in our estimates. Not wanting to take them at their word, I recently ran my own version of their tests. Around 30 people responded to the following two tests:
- Ten 90% Confidence Interval questions
- Ten binary questions
90% Confidence Interval questions are similar to the rainfall questions above: you should be 90% confident that the correct answer will be between your lower and upper bounds. As a result, we expect the ranges given to contain the correct answer nine times out of ten (i.e. correct 90% of the time).
A binary question asks you to say whether a statement is true or false AND declare how confident you are in your answer. For example, “Wanderers beat Royal Engineers in the first ever FA Cup Final in 1872”. Is that true or false? If you have no idea and choose true or false at random, then you would say you are 50% confident (like the toss of a coin). If you are absolutely certain in your true or false answer, then you are 100% confident. Or, depending on your knowledge of the area, you may be 60%, 70%, 80% or 90% confident. The number of binary questions we expect a respondent to get right depends on their stated confidence levels: we add up their confidence ratings for the ten questions, then divide it by 100. For example, if I gave a 50% rating for 8 questions, and 100% for 2 questions, then I should get 6 answers correct (600/10). Fewer correct answers would suggest over-confidence; more correct answers shows under-confidence.
What results did I get?
Like Hubbard and McConnell, my participants were over-confident. Whilst most people in their experiments got 3 out of 10 correct for the 90% confidence interval tests, we peaked at 5 out of 10 (although the higher figure was probably because I allowed people to do research before giving an answer). Similarly, nearly everyone was over-confident in the binary questions too.
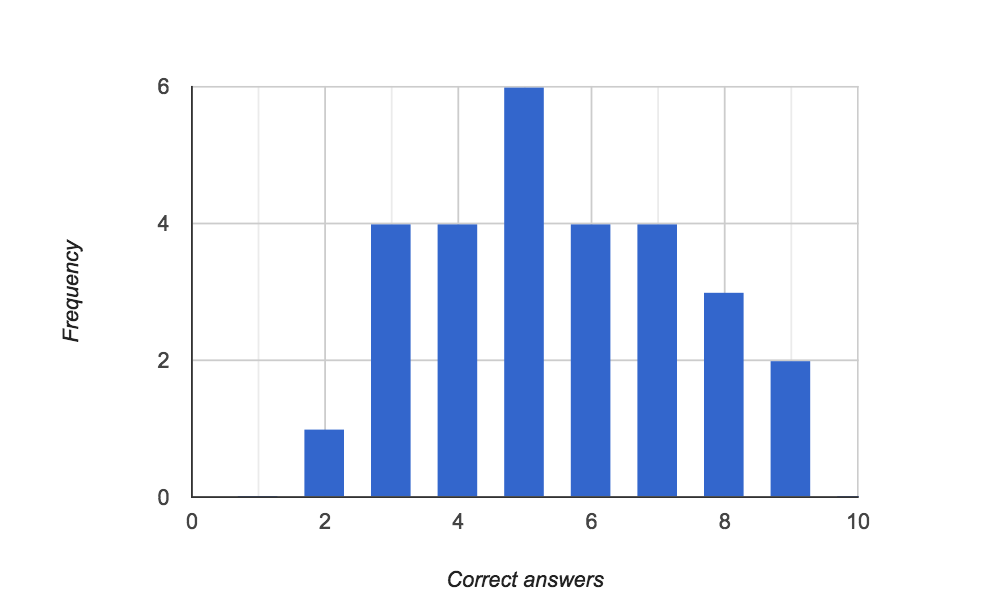
90% Confidence Interval results showing over-confidence: everyone should have got 9/10 correct answers.
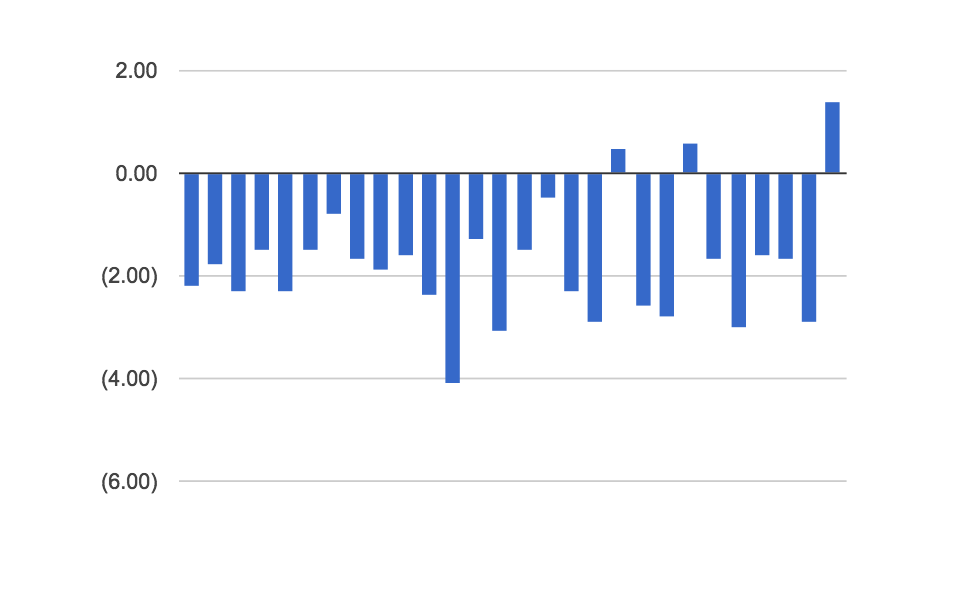
Binary questions showing over-confidence: 0.00 represents the baseline that each respondent anticipated getting correct (e.g. 0.00 would be 6 correct answers for the example above).
Is there any hope?
“… studies have shown that very few people are naturally calibrated estimators” ~ Douglas Hubbard
Steve McConnell and Douglas Hubbard have shown that, with practice, people can improve their estimation skills by ‘calibrating’ their estimation skills. You do this by estimating general questions such as “what is the surface temperature of the sun”. According to Hubbard, estimating is a skill that can be learned and “transfers to any area of estimation.”
So how do you go about getting better? I’d suggest reading the books by Hubbard and McConnell, but here are a few pointers to get you started:
- Start with an absurdly wide range … then start eliminating the values you know to be extremely unlikely;
- Practice and get feedback. Start with the test that I blogged about back in January 2014 then repeat with the other tests in their books. Or write your own and practice with friends and colleagues;
- Don’t make assumptions within your estimates; your ranges and confidence ratings should account for such uncertainties;
- Try to think of two reasons why you should be confident in your estimate and two reasons why it might be wrong. Then ask whether you should revise your answer.
