What is Little’s Law?
If you have a stable system (e.g. one-in-one-out), then the average number of customers you have within that system is equal to the average rate of customer arrivals multiplied by the average time a customer spends in the system. That was the law proposed by John Little in the mid-1900s.
This is commonly expressed as L = λW (where “L” is the average number of customers, “λ” is average arrival rate and “W” is the average time in the system).
Popular in queueing theory, the law proves that when you increase the number of customers in the system, and keep the arrival rate constant, the average time in the system increases. In short, increasing the number of customers means that it takes longer for each one to be served.
Maybe you remember from school, that you can rework L = λW to show that λ = L / W and W = L / λ
Why do we care?
We slightly redefine the terms as follows:
- average number of customers becomes average items of work in progress (WIP)
- average arrival rate becomes average delivery rate (DR) – we can change this because arrival and departure time will be the same in a stable one-in-one-out system
- average time in the system, the average time it takes to go from start to finish, is known to us as lead time (LT)
For us, Little’s Law tells us that WIP = DR x LT (which can also be expressed as DR = WIP / LT and LT = WIP / DR).
We can then use Little’s Law to prove that increasing the average amount of work in progress (WIP) has the effect of increasing the average time it takes for each work item to be completed (Lead Time).
For example:
We have an average of 6 work items in progress, an average delivery rate of 2 items per day, and an average lead time of 3 days.
- WIP = DR x LT
- 6 = 2 x 3
If you remember your childhood lessons on refactoring algebra, this can also be expressed as:
- LT = WIP / DR
- 3 = 6 / 2
Using this refactored equation, we can see what happens to lead time if we increase WIP to 12:
- LT = WIP / DR
- LT = 12 / 2
- LT = 6
Lead time increases from 3 days to 6 days.
But doesn’t this also prove that increasing WIP can increase Delivery Rate?
If we take our initial example, increase WIP to 12 but keep lead time as 3 days, then we get:
- DR = WIP / LT
- DR = 12 / 3
- DR = 4
By increasing WIP, we have also increased delivery rate! Isn’t this a good thing?
Although that might be true from an algebraic perspective, it’s not what usually happens. If I doubled your workload, you’re unlikely to suddenly become twice as productive and complete it in the same time; you will just take twice as long to complete twice as much work, delivering at about the same rate as before*.
So, in short, Little’s Law tells us: if you increase WIP, without finding a way of increasing delivery rate, then your lead time will increase. Conversely, it tells us that decreasing WIP may reduce lead time.
Want to see this in action? Check out my video WIP: why limiting work in progress makes sense
Also, why not take our quiz about Little’s Law?
[* In fact, due to context switching, your delivery rate will probably drop slightly too]
OUT NOW!
The Innovation Revelation: A story about how to satisfy customer needs.
A real-world guide to taking a customer-focused approach to creating products and services that people actually want and are happy to pay for.

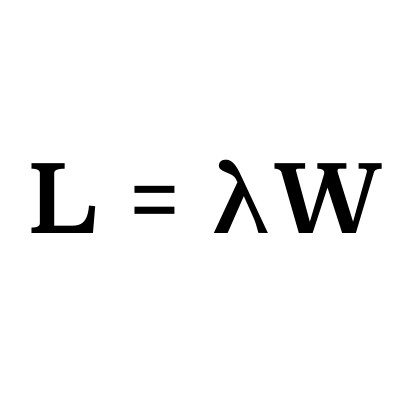
Pingback: Probabilistic Forecasting | Scrum & Kanban
Nicely explained.